12. Multiclass Entropy
Multi-class Entropy
Last time, you saw this equation for entropy for a bucket with m red balls and n blue balls:
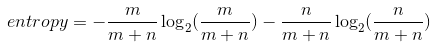
We can state this in terms of probabilities instead for the number of red balls as p_1 and the number of blue balls as p_2:
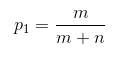
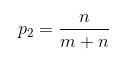
entropy = -p_1\log_2(p_1)-p_2\log_2(p_2)
This entropy equation can be extended to the multi-class case, where we have three or more possible values:
entropy = -p_1\log_2(p_1) - p_2\log_2(p_2) - … - p_n\log_2(p_n) = -\sum\limits_{i=1}^n p_i\log_2(p_i)
The minimum value is still 0, when all elements are of the same value. The maximum value is still achieved when the outcome probabilities are the same, but the upper limit increases with the number of different outcomes. (For example, you can verify the maximum entropy is 2 if there are four different possibilities, each with probability 0.25.)